Research
PhD Subject
Keywords: Nonlocal games, Communication complexity, Quantum Cryptography.
Communication complexity quantifies how difficult is a Boolean function $f(X, Y)$ to be computed by two distant parties, Alice and Bob, knowing that each party receives only half of the inputs, and under the constraint of communicating as few bits as possible [Yao79, KN96]. In some rare cases, only one bit of communication is enough to evaluate $f$, in which case we say that communication complexity collapses, see the following figure:
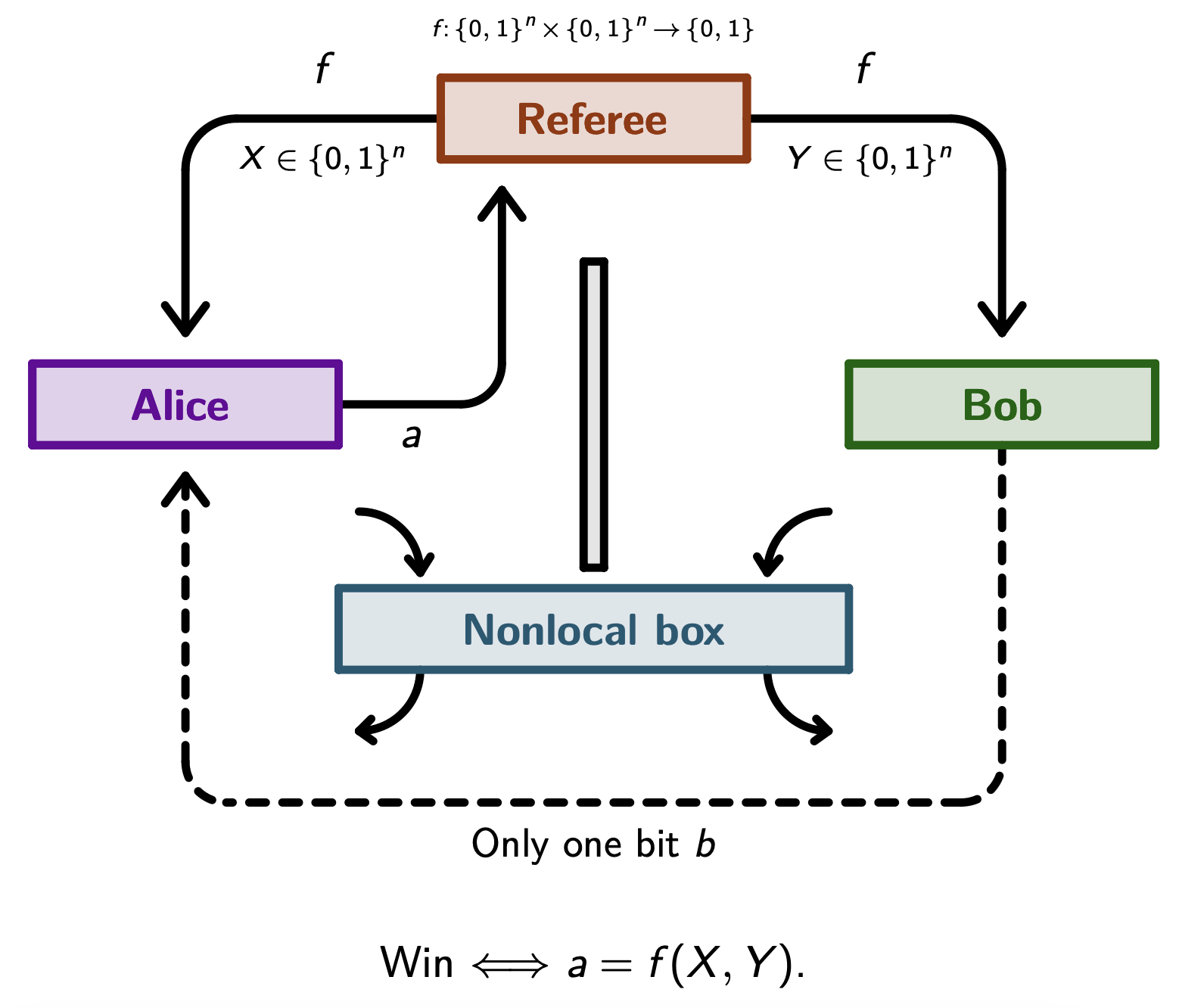
Previous image from [BBP23]. It would be very surprising to find in Nature a resource that collapses communication complexity for any Boolean function $f$ with arbitrary entry size, since it would be too powerful to being able to correctly estimate the value of any Boolean function with only one bit of communication.
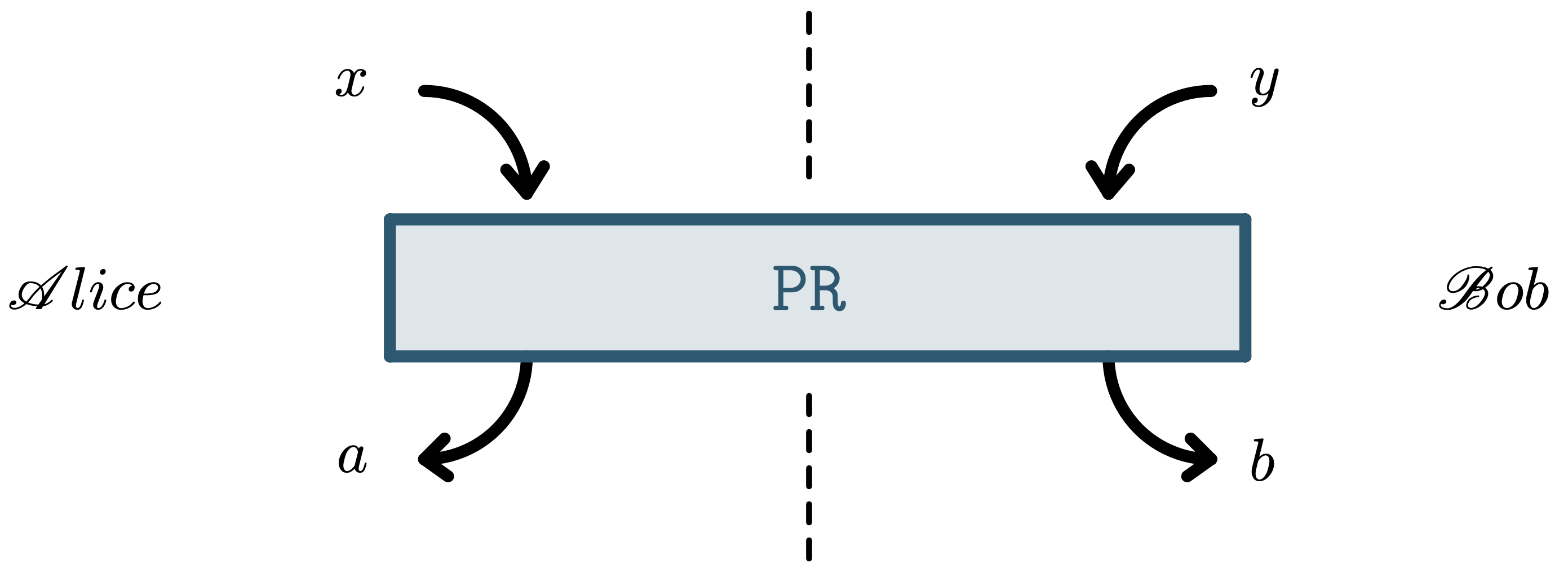
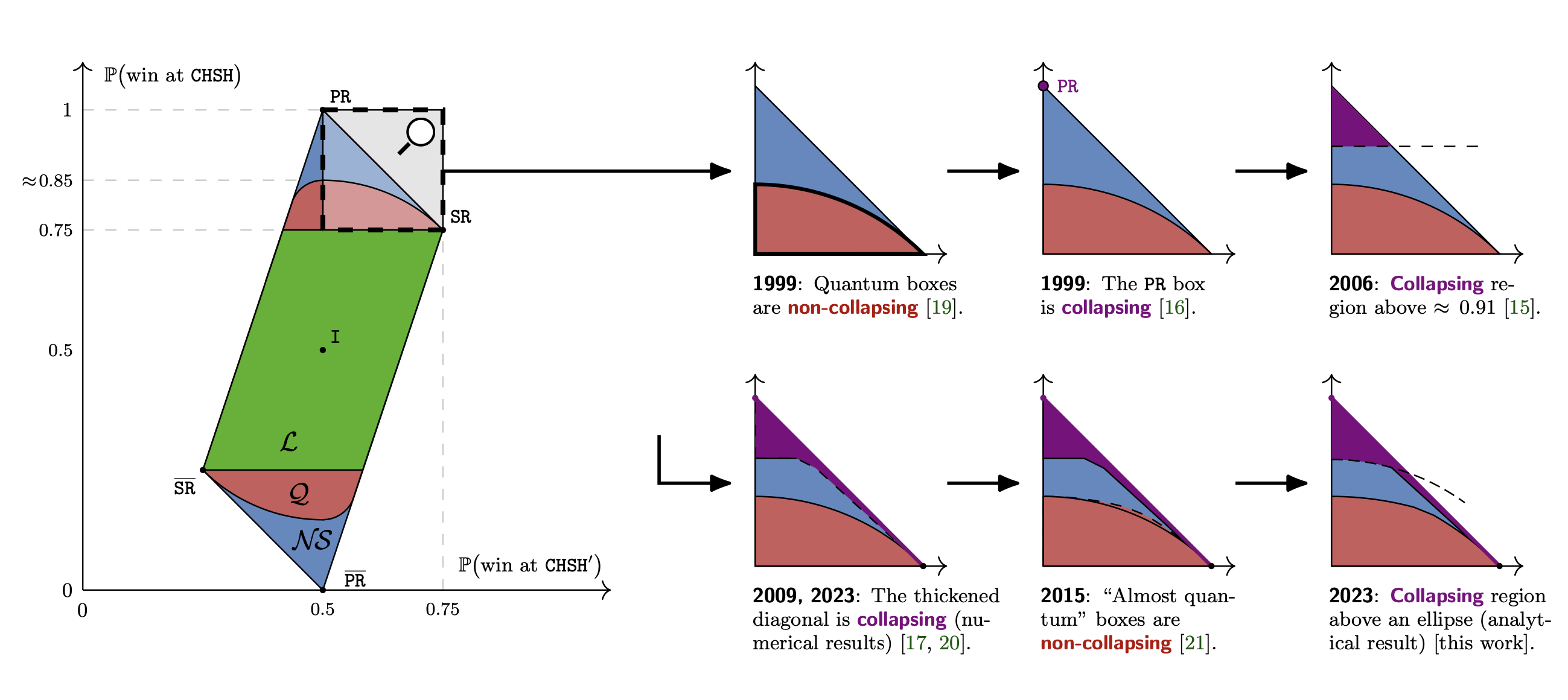
Previous image from [BBP23]. In our work, we reduce the unknown gap by finding new nonlocal boxes that collapse communication complexity, see our articles.
PhD Supervisors
My supervising team is composed of three complementary perspectives of Quantum Information Theory:- Anne Broadbent (University of Ottawa), an expert in quantum cryptography, quantum nonlocality, and quantum complexity theory. See the quantum team in Ottawa.
- Ion Nechita (CNRS, University of Toulouse), an expert in random matrix theory, with a recent focus on the theory of random tensors, and in the theory of quantum entanglement.
- Clément Pellegrini (University of Toulouse), an expert on stochastic aspects of quantum mechanics, with a focus on the theory of quantum trajectories and open quantum systems. See the quantum team in Toulouse.
More details
Icons provided by FontAwesome. LaTeX equations displayed using MathJax.